18. 基于时间的反向传播算法(第三部分)
最后一步!调整连接状态和输出的权重矩阵W_x。
如果你接受了之前独立推导数学的挑战,坐好,系好安全带,并对比你和我们的注释!不要担心犯错,我们都会犯错。你的错误将帮助你下一步避免犯错。
21 循环神经网络:基于时间的反向传播算法 C V7 最后一节
调整W_x所需的梯度计算
为了进一步理解基于时间的反向传播算法过程,我们将再次简化展开模型。这次侧重于W_x对输出的贡献上,方法如下:
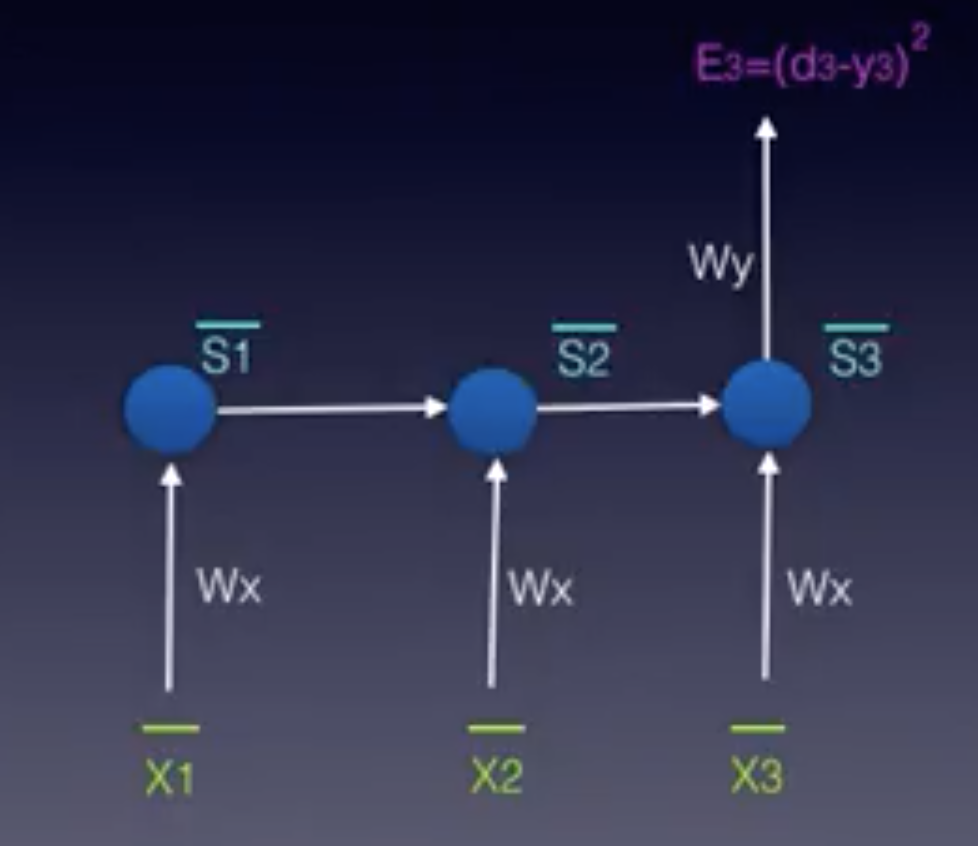
用于调整Wx的简化展开模型
计算W_x损失函数的偏导数时,我们需要再次考虑所有对输出有贡献的状态。与我们之前见到的一样,在这个例子中,状态\bar{s_3}取决于之前的状态\bar{s_2},而之前的状态也取决于前面的\bar{s_1},即第一个状态。
正如我们前面所说,在基于时间的反向传播算法中,我们将考虑每个状态中的每个梯度,累加所有贡献。
- 时间步长 t=3 时,来自\bar{s_3}的梯度贡献如下:
(请注意这里使用链式法则。如果需要,请返回视频查看计算路径)。
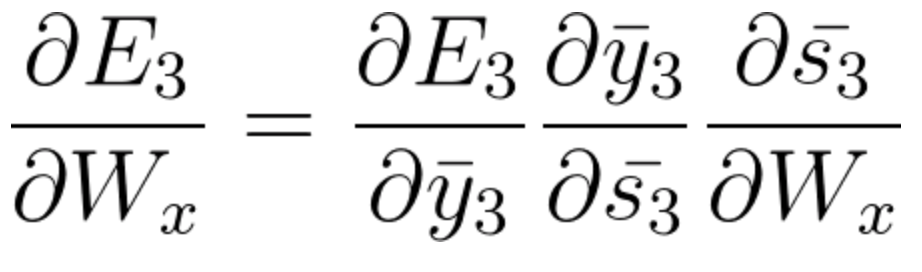
方程式43
- 时间步长 t=3 时,来自\bar{s_2}的梯度贡献如下:
(请注意,链式法则推导的方程式如何考虑\bar{s_2}对\bar{s_3}的贡献。如果需要,请返回视频查看计算路径)。
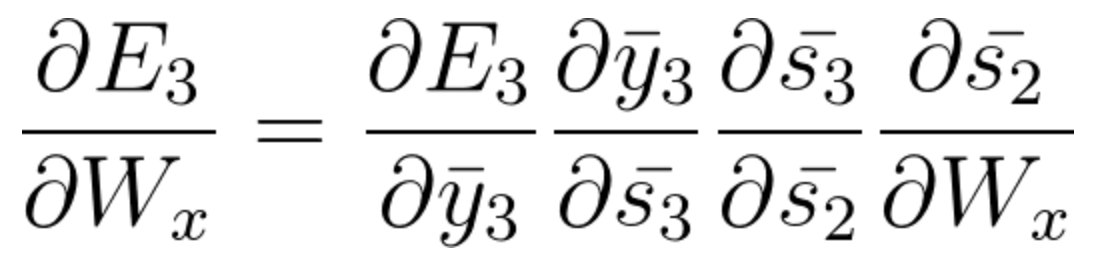
方程式44
- 时间步长 t=3 时,来自 \bar{s_1}的梯度贡献如下:
(请注意,链式法则推导的方程式如何考虑\bar{s_1}对\bar{s_2} and \bar{s_3}的贡献。如果需要,请返回视频查看计算路径)。
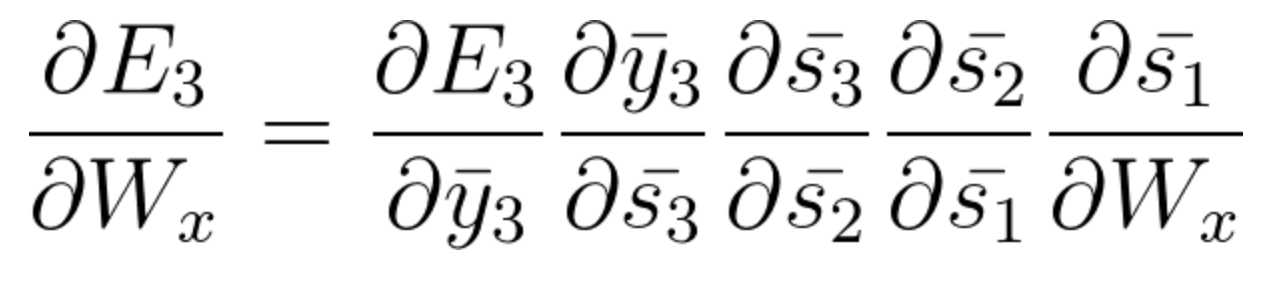
方程式45
考虑以下三个状态的贡献后:\bar{s_3}、\bar{s_2}和\bar{s_1},我们要累加它们,找到最终的梯度计算。
下列方程式使用基于时间的反向传播算法,调整W_x的梯度:
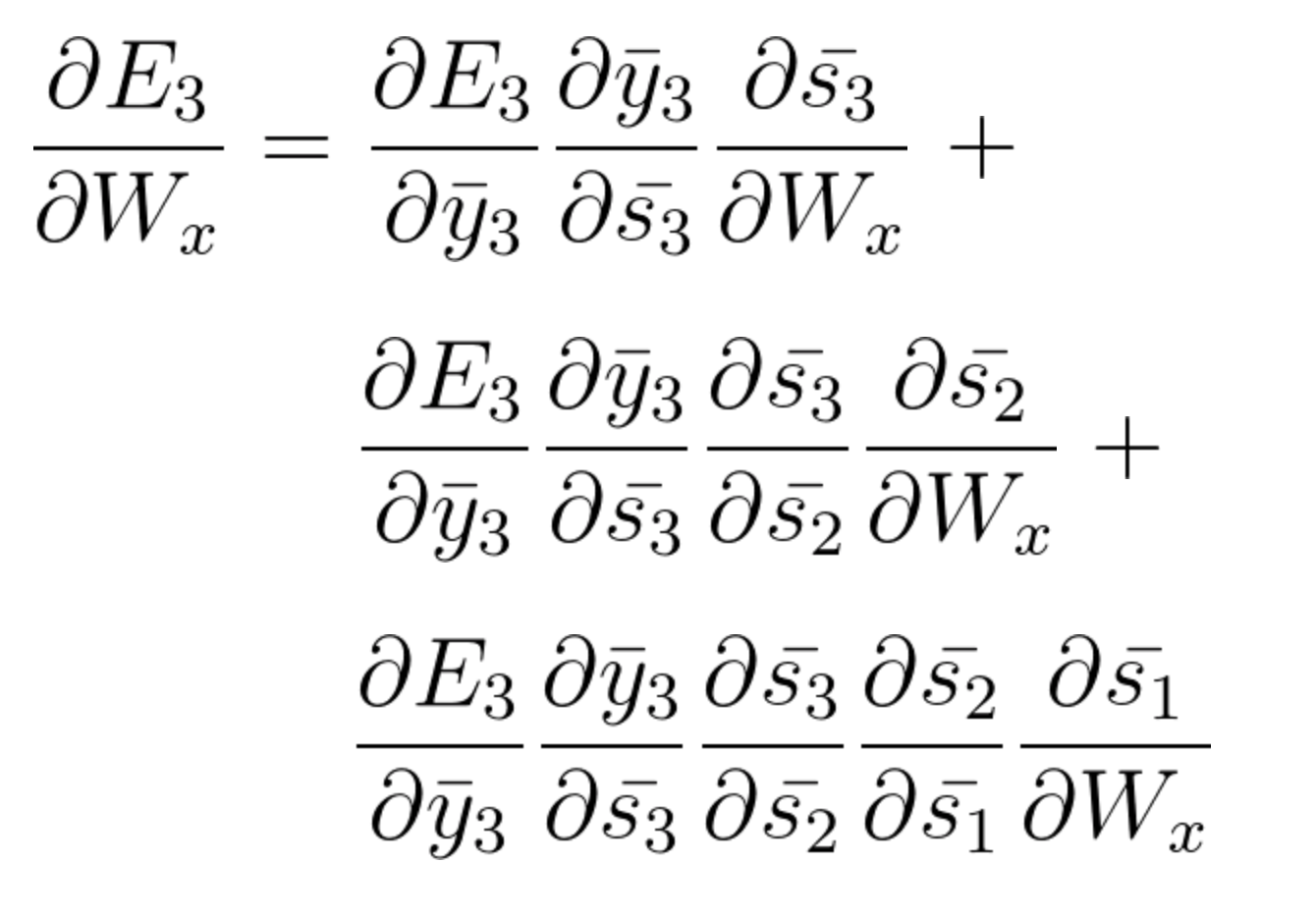
方程式46
这个例子中,我们需要考虑三个时间步长,所以我们累加了三个偏导数进行计算。一般来说,我们可以追溯多个时间步长。如果仔细观察方程式43、44和45,你将再次注意到一种模式。当反向退后一步,我们在链式法则中就需要考虑一个额外的偏导数。从数学角度上来说,这可以用下面的通用方程式表示,使用基于时间的反向传播算法来调整W_x:
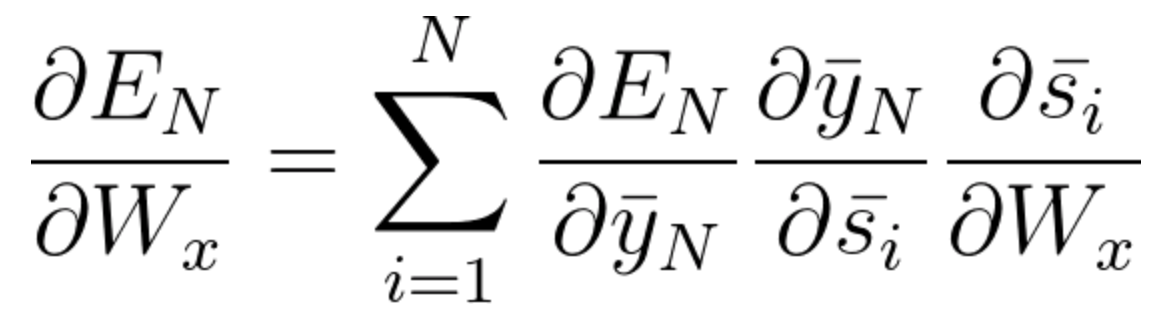
方程式47
请注意\frac{\partial{E_3} }{\partial W_s} 和 \frac{\partial{E_3} }{\partial W_x}计算的相似性。希望理解\frac{\partial{E_3} }{\partial W_s}计算过程后,再去理解\frac{\partial{E_3} }{\partial W_x}就非常简单。